Zero Shot问题是指：
有一组大量labelled data，定义为$(x^s, y^s)$
有一组少量unlabelled data，定义为$(x^t)$
通过$(x^s, y^s)$和$(x^t)$来预测$(y^t)$，但$(x^t)$没有出现在$(x^s)$中。

1. 方法一：以另一种方式分class

在语音识别任务中，每个单词可以看作是一个class。有可能要识别的单词没有出现在训练集中。
解决方法：以单词为class -> 以音位phonemes为class
phonemes是可以穷举的。

1. 通过NN把语音转成phonemes。
2. 通过预先定义好的table，把phonemes转成单词。

在语音识别任务中，训练集是猫、狗，测试集出现草泥马：

解决方法：以名字作为class -> 以特征作为class

1. 分析图像中的动物的特征，例如毛、腿、尾等。
2. 通过预先定义好的table，根据特征推测动物的名字。

2. 方法二：attribute embedding

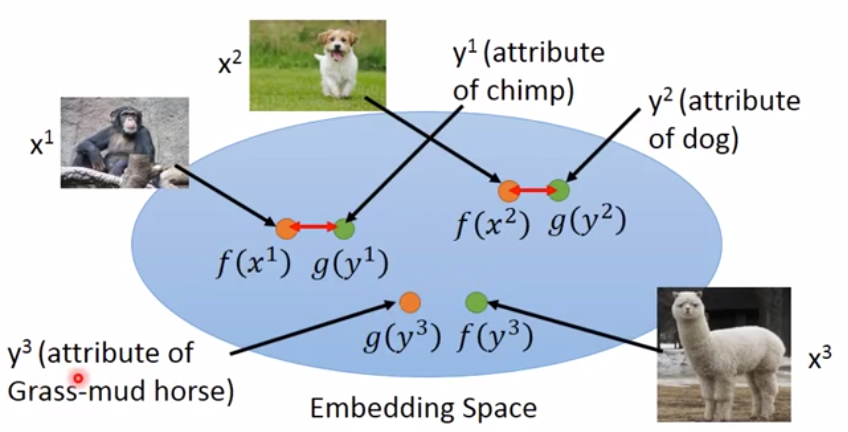
f()将图像转成向量。
g()将特征转成向量。
f和g都通过NN训练得到，训练的目标是$f(x^n)$和$g(y^n)$越接近越好。
也可以用动物的名字代替特征（attribute embedding + word embedding）：

定义loss function如下：
$\begin{aligned} L = \sum_n max\left(0, k-f(x^n)g(y^n) + max_{m\neq n}f(x^n)g(y^n) \right) && (1)\\ f*, g* = \arg\min_{f,g} L && (2) \end{aligned}$

目标是要最小化L。当max{}的第二项小0时，L取到最小值0。即：
$\begin{aligned} f(x^n)g(y^n) - max_{m\neq n}f(x^n)g(y^n) > k && (3) \end{aligned}$

公式(3)左边第一项代表：$f(x^n)$和$g(y^n)$应尽量接近
公式（3）左边第二项代表：$f(x^n)$和$g(y^m)$应尽量远离

3. 方法三：Convex Combination of Sematic Embedding

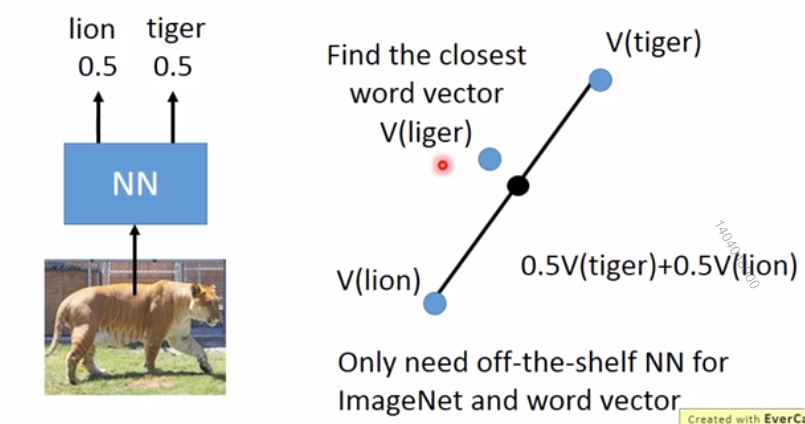
假设有一张图像，NN的分类结果为：P(lion) = 0.5, P(tiger) = 0.5

1. 找到向量$V_{tiger}$和$V_{lion}$
2. 计算向量$v = P(lion)V_{lion} + P(tiger)V_{tiger}$
3. 找到离v最近的标签，因此得到liger
4. 图像分类为liger