He et.al., 2015. Deep residual networks for image recognitisn

1. 什么是残差网络

1.1. Residual Block

正常的网络层是这样的：

$\begin{aligned} z^{[l+1]} = W^{[l+1]}a^{[l]} + b^{[l]} \\ a^{[l+1]} = g(z^{[l+1]}) \\ z^{[l+2]} = W^{[l+2]}a^{[l+1]} + b^{[l+1]} \\ a^{[l+2]} = g(z^{[l+2]}) \end{aligned}$

残差块是这样的：

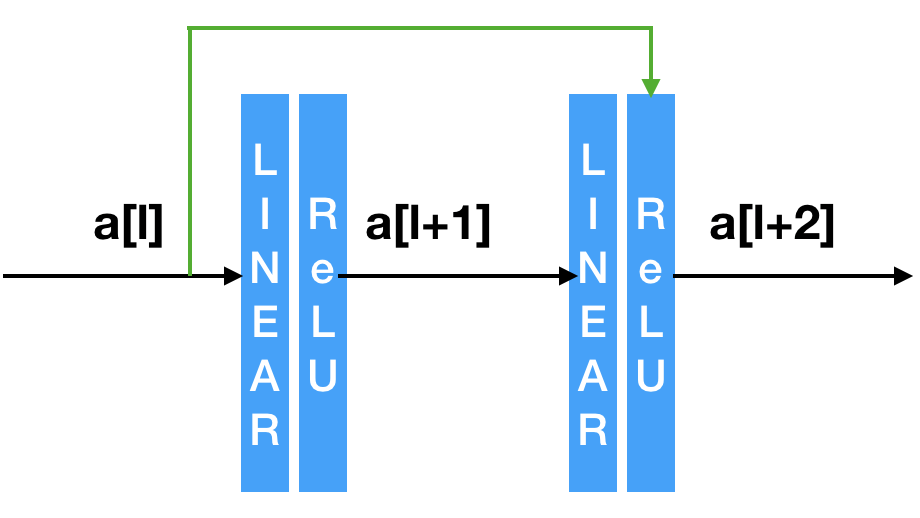
图中黑色的线称为main path，绿色的线称为short cut/skip connection。
公式的变化体现在最后一行:

$\begin{aligned} z^{[l+1]} = W^{[l+1]}a^{[l]} + b^{[l]} \\ a^{[l+1]} = g(z^{[l+1]}) \\ z^{[l+2]} = W^{[l+2]}a^{[l+1]} + b^{[l+1]} \\ a^{[l+2]} = g(z^{[l+2]} + a^{[l]}) \end{aligned}$

残差块使网络可以更深。网络深度与训练集性能的关系：

1.2. Residual Network

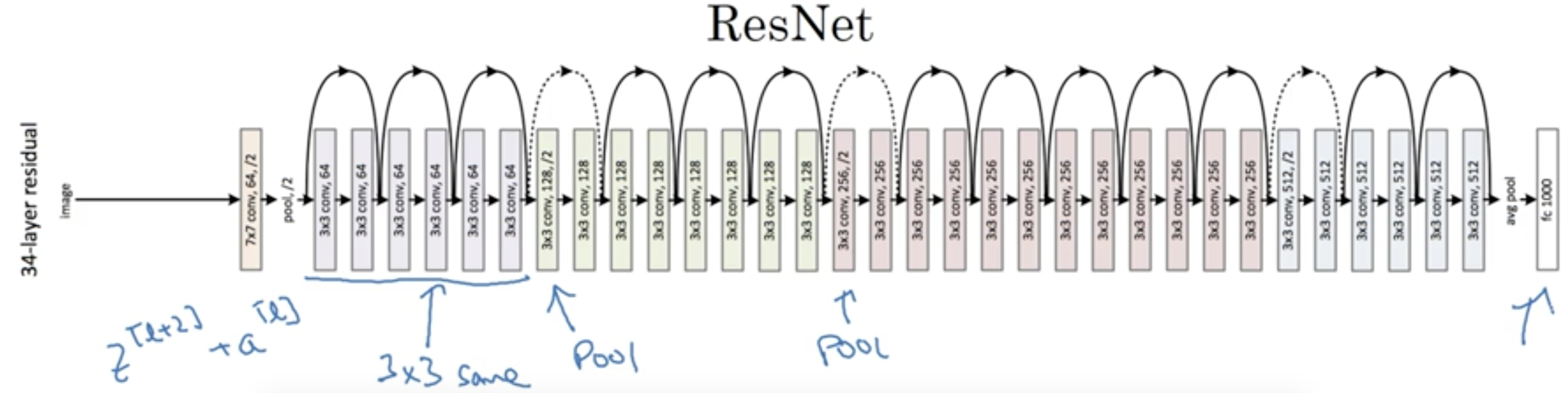
2. 为什么残差网络有用？

$\begin{aligned} a^{l+2} &=& g(z^{l+2} + a^l) \\ &=&g(W^{l+2}a^{l+1} + b^{l+2} + a^l) && (1) \\ &=& g(a^l) && (2) \\ &=& a^{l} && (3) \end{aligned}$

(1) 由于L2 正则化的影响,W会shrink,假设此时W=0
(2) 假设g使用ReLU (3) 根据以上公式$a^{L+2}$可以很容易地得到与a^l相同的结果。（性能不变）。因此在一个深的NN上增加一个residual block，至少不会对性能有坏处。
运气好的话，a^{l+2}能得到比$a^l$好的结果。（性能提升）

3. 其它

因为$a^{l+2} = g(z^{l+2} + a^l)$使用残差块用的跳跃连接，要求使用same卷积。使$a^l$与z^{l+2}有相同的维度。
或者将$a^l$映射到$z^{l+2}$的大小：

$a^{l+2} = g(z^{l+2} + Wa^l)$