深度学习算法在许多情况下都涉及到优化。 例如，模型中的进行推断（如\,PCA）涉及到求解优化问题。 我们经常使用解析优化去证明或设计算法。 在深度学习涉及到的诸多优化问题中，最难的是神经网络训练。 甚至是用几百台机器投入几天到几个月来解决单个神经网络训练问题，也是很常见的。 因为这其中的优化问题很重要，代价也很高，因此研究者们开发了一组专门为此设计的优化技术。 本章会介绍神经网络训练中的这些优化技术。

如果你不熟悉基于梯度优化的基本原则，我们建议回顾第4章。 该章简要概述了一般的数值优化。

本章主要关注这一类特定的优化问题：寻找神经网络上的一组参数$\theta$，它能显著地降低代价函数 $J(\theta)$，该代价函数通常包括整个训练集上的性能评估和额外的正则化项。

[success]
deep network定义了一个function space。
另外定义了一个代价函数来评价一个function的好坏。
假设在function space中最好的function为f。
从function space从找到f的过程称为Optimization。

首先，我们会介绍在机器学习任务中作为训练算法使用的优化与纯优化有哪些不同。 接下来，我们会介绍导致神经网络优化困难的几个具体挑战。 然后，我们会介绍几个实用算法，包括优化算法本身和初始化参数的策略。 更高级的算法能够在训练中自适应调整学习率，或者使用代价函数二阶导数包含的信息。 最后，我们会介绍几个将简单优化算法结合成高级过程的优化策略，以此作为总结。

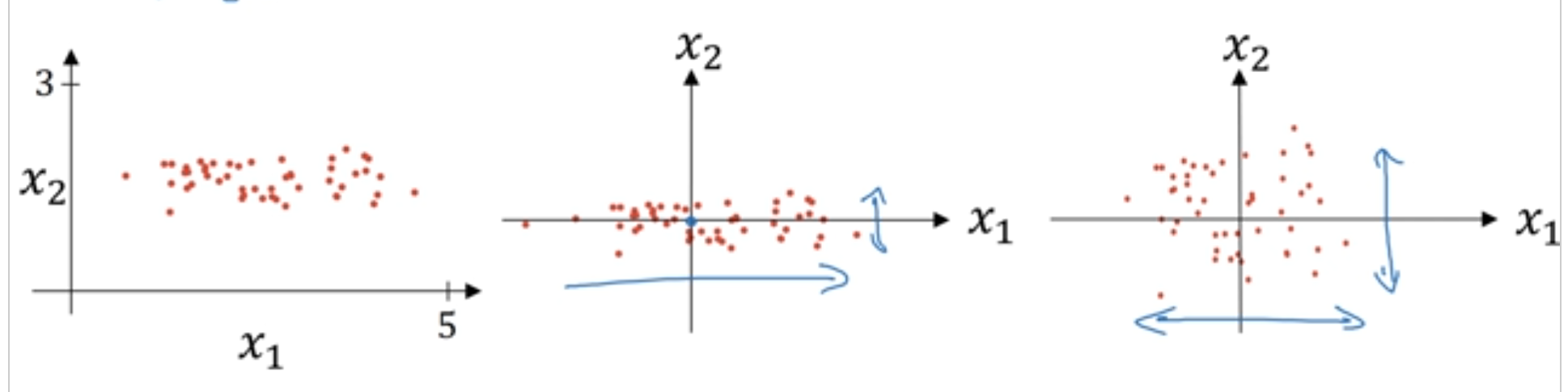
正则化输入
这一段内容是Ag的视频课上讲的，不知道放哪，就放这里了。
输入数据的正则化 = 零均值化 + 方差归一化
$x_i^r = \frac{x_i^r - \mu_i}{\sigma_i}$

优点：可以加速训练
注意：训练集做计算出来的用于归一化的均值和方差要记下来，测试集不能使用自己的均值和方差，而应该使用训练集的均值和方差。
原理：归一化之后，所有特征都在同一尺度下 ==> J更圆 ==> 更容易优化