学习循环网络长期依赖的数学挑战在第8.2.5节中引入。

[success] Ag补充
The cat, ..., was full.
The cats, ..., were full.
两个句子中，中间的省略号可能很长。cat/cats对was/were的影响就是长期依赖。
由于梯度消失问题的存在，很难让NN意识到它要记住前面看到的是单数名词还是复数名词，并在后面使用正确的单复数形式。

[success]
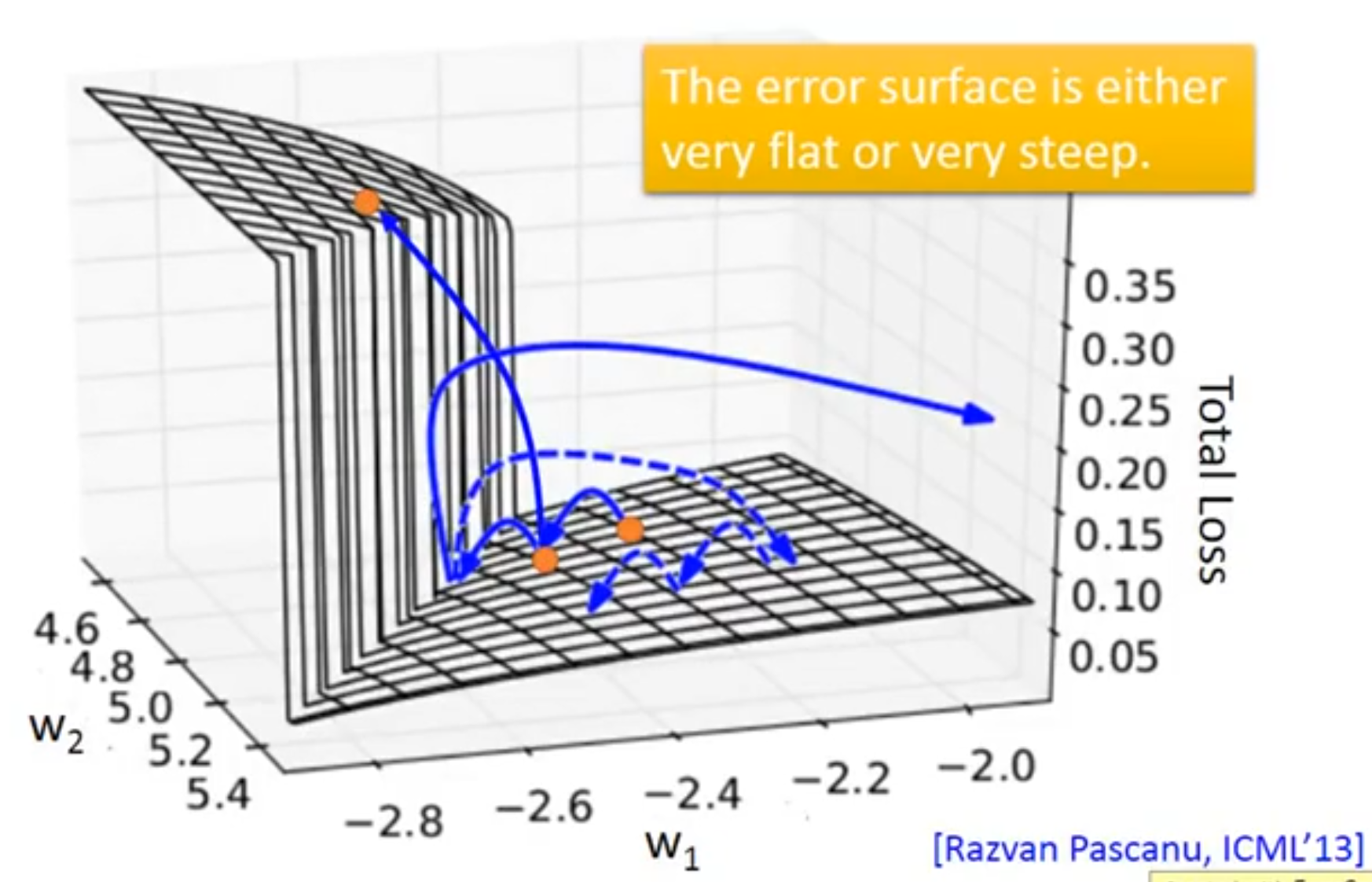
RNN的loss曲线很有可能是这样的：

问：为什么RNN的loss会剧烈地抖动？
答：RNN的error surface要么很平(梯度消失)，要么很陡（梯度爆炸），陡峭的地方称为悬崖。

问：梯度消失有什么问题？
梯度变得很小，不能指导优化的方向。
解决方法：可存储记忆。
问：梯度爆炸有什么问题？
答：如果从悬崖下面update到悬崖上面，loss就会陡增。
如果点正好落在悬崖上，梯度会突然非常大，然后参数就飞出去了。
解决方法：梯度截断
问：为什么LSTM能解决梯度消失的问题？20'15''
答：RNN和LSTM处理memory cell的操作不同。
在RNN中，t时刻计算出的值直接存入memory cell中，覆盖t-1时刻的值。
而在LSTM中，新memory = 旧memory * Gate + input。
可见，只有Forget Gate不关闭，weight对memory的影响将永远存在。
因此在实际训练过程中，应该将forget Gate设计为，在大多数情况下，forget gate都是开着的。

根本问题是，经过许多阶段传播后的梯度倾向于消失（大部分情况）或爆炸（很少，但对优化过程影响很大）。

[success]
梯度爆炸更容易发现，因为它会导致参数太大而崩溃。
梯度爆炸可以使用梯度截断clipping来解决。
相比之下，梯度消失的问题更难发现和解决。

即使我们假设循环网络是参数稳定的（可存储记忆，且梯度不爆炸），但长期依赖的困难来自比短期相互作用指数小的权重（涉及许多Jacobian相乘）。

[warning] 可存储记忆可解决梯度消失问题。既然假设梯度消失已解决，梯度爆炸不存在，还讨论啥？“比短期相互作用指数小的权重”是什么？

许多资料提供了更深层次的讨论{cite?}。 在这一节中，我们会更详细地描述该问题。 其余几节介绍克服这个问题的方法。

循环网络涉及相同函数的多次组合，每个时间步一次。 这些组合可以导致极端非线性行为，如\fig?所示。

特别地，循环神经网络所使用的函数组合有点像矩阵乘法。 我们可以把如下的循环联系
$\begin{aligned} h^{(t)} = W^\top h^{(t-1)} \end{aligned}$

看做是一个非常简单的、缺少非线性激活函数和输入$x$的循环神经网络。 如\sec?描述，这种循环关系本质上描述了幂法。 它可以被简化为
$\begin{aligned} h^{(t)} = (W^t)^\top h^{(0)}, \end{aligned}$

而当$W$符合下列形式的特征分解
$\begin{aligned} W = Q \Lambda Q^\top, \end{aligned}$

其中$Q$正交，循环性可进一步简化为
$\begin{aligned} h^{(t)} = Q^\top Lambda^t Q h^{(0)}. \end{aligned}$

特征值提升到$t$次后，导致幅值不到一的特征值衰减到零，而幅值大于一的就会激增。 任何不与最大特征向量对齐的$h^{(0)}$的部分将最终被丢弃。

这个问题是针对循环网络的。

[success] 问：为什么循环网络会有这样的问题？
解释一：因为sigmoid unit?老师说不是这个原因。
在前馈网络中，在hidden layer中使用sigmoid unit会导致这种情况。sigmoid unit->ReLU就能解决这个问题。
解释二：推导BPTT的公式可以分析出来原因。老师没有展开讲这部分内容。
解释三：直观分析
假设有这样一个toy example。

w的梯度= $\delta w$ 对$\delta C$的影响。
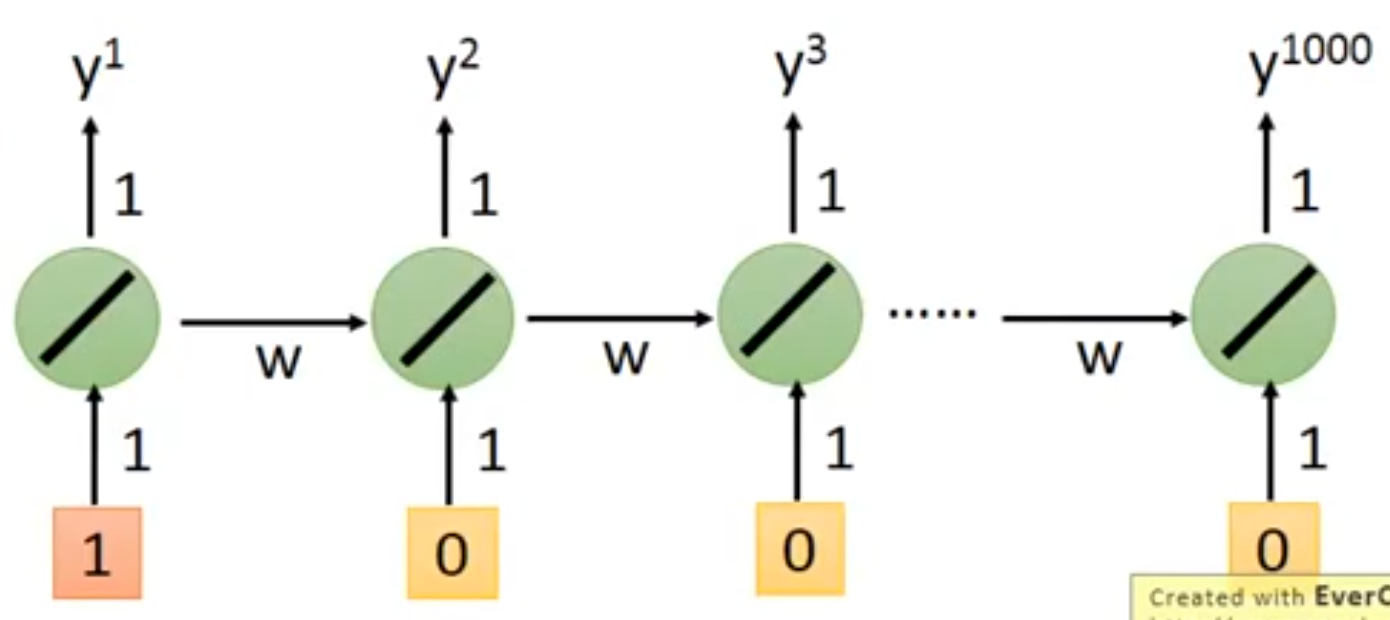
构造图中这样的一个简单的RNN，令unit的输入w为1，输出w为1，只在t0时刻有一个输入，值为1。观察unit的transition weight对C的影响。
令w=1，则y1000=1
w=1.01, y1000=20000 -- 悬崖 w=0.99, y1000=0 --- 平坦 w一但有影响，影响就是天崩地裂。这是因为同样的w在transition过程中反复使用。放大了它的作用。
解决方法LSTM。
LSTM只能解决梯度消失的问题，不能解决梯度爆炸的问题。悬崖仍然存在，通常将lr设置得比较小。

在标量情况下，想象多次乘一个权重$w$。 该乘积$w^t$消失还是爆炸取决于$w$的幅值。 然而，如果每个时刻使用不同权重$w^{(t)}$的非循环网络，情况就不同了。 如果初始状态给定为$1$，那么时刻$t$的状态可以由$\prod_t w^{(t)}$给出。 假设$w^{(t)}$的值是随机生成的，各自独立，且有$0$均值$v$方差。 乘积的方差就为$\Bbb O(v^n)$。 为了获得某个期望的方差$v^*$，我们可以选择让单个权重的方差为$v=\sqrt[n]{v^*}$。 因此，非常深的前馈网络通过精心设计的比例可以避免梯度消失和爆炸问题，如{Sussillo14}所主张的。

[success]
非循环网络每个时刻的$w^{(t)}$不同，通过合理设计$w^{(t)}$，可以避免梯度消失和爆炸问题。

RNN梯度消失和爆炸问题是由不同研究人员独立发现{cite?}。 有人可能会希望通过简单地停留在梯度不消失或爆炸的参数空间来避免这个问题。 不幸的是，为了储存记忆并对小扰动具有鲁棒性，RNN必须进入参数空间中的梯度消失区域{cite?}。 具体来说，每当模型能够表示长期依赖时，长期相互作用的梯度幅值就会变得指数级小（相比短期相互作用的梯度幅值）。 这并不意味着这是不可能学习的，由于长期依赖关系的信号很容易被短期相关性产生的最小波动隐藏，因而学习长期依赖可能需要很长的时间。 实践中，{Bengio1994ITNN}的实验表明，当我们增加了需要捕获的依赖关系的跨度，基于梯度的优化变得越来越困难，SGD在长度仅为10或20的序列上成功训练传统RNN的概率迅速变为0。

[warning] 这一整段看不懂

将循环网络作为动力系统更深入探讨的资料见{Doya93,Bengio1994ITNN,Siegelmann+Sontag-1995}及 {Pascanu-et-al-ICML2013}的回顾。 本章的其余部分将讨论目前已经提出的降低学习长期依赖（在某些情况下，允许一个RNN学习横跨数百步的依赖）难度的不同方法，但学习长期依赖的问题仍是深度学习中的一个主要挑战。