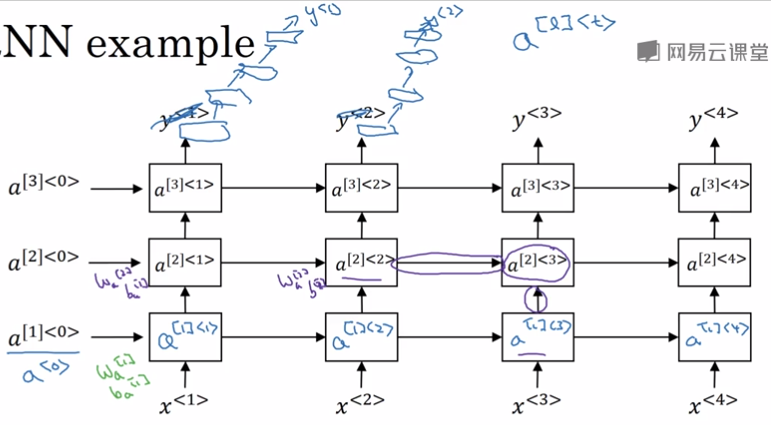
大多数RNN中的计算可以分解成三块参数及其相关的变换：

• 从输入到隐藏状态，
• 从前一隐藏状态到下一隐藏状态，以及
• 从隐藏状态到输出。 根据\fig?中的RNN架构，这三个块都与单个权重矩阵相关联。 换句话说，当网络被展开时，每个块对应一个浅的变换。 能通过深度MLP内单个层来表示的变换称为浅变换。

  [success]
  一个层 = 仿射变换 + 一个固定的非线性表示组
  Wx这样的操作就是仿射变换。
  激活函数就是非线性表示组。
  f(Wx + b)这样的计算一次相当于一个层。
  Ag补充：
  定义$a^{l,t}$为时刻t第l层的activation。
  $a^{l,t} = g(W_a^l[a^{l,t-1}, a^{l-1,t}] + b_a^l)$

通常，这是由学成的仿射变换和一个固定非线性表示组成的变换。

在这些操作中引入深度会有利的吗？ 实验证据{cite?}强烈暗示理应如此。 实验证据与我们需要足够的深度以执行所需映射的想法一致。 读者可以参考{Schmidhuber92,ElHihi+Bengio-nips8}或{Jaeger2007}了解更早的关于深度RNN的研究。

{Graves-et-al-ICASSP2013}第一个展示了将RNN的状态分为多层的显著好处，如\fig?\emph{(左)}。 我们可以认为，在图10.13(a)所示层次结构中较低的层起到了将原始输入转化为对更高层的隐藏状态更合适表示的作用。 {Pascanu-et-al-ICLR2014}更进一步提出在上述三个块中各使用一个单独的MLP（可能是深度的），如图10.13(b)所示。

[warning] 这三块的分别变深有什么区别？不都是增加隐藏层数吗？

考虑表示容量，我们建议在这三个步中都分配足够的容量，但增加深度可能会因为优化困难而损害学习效果。

[success] Ag补充
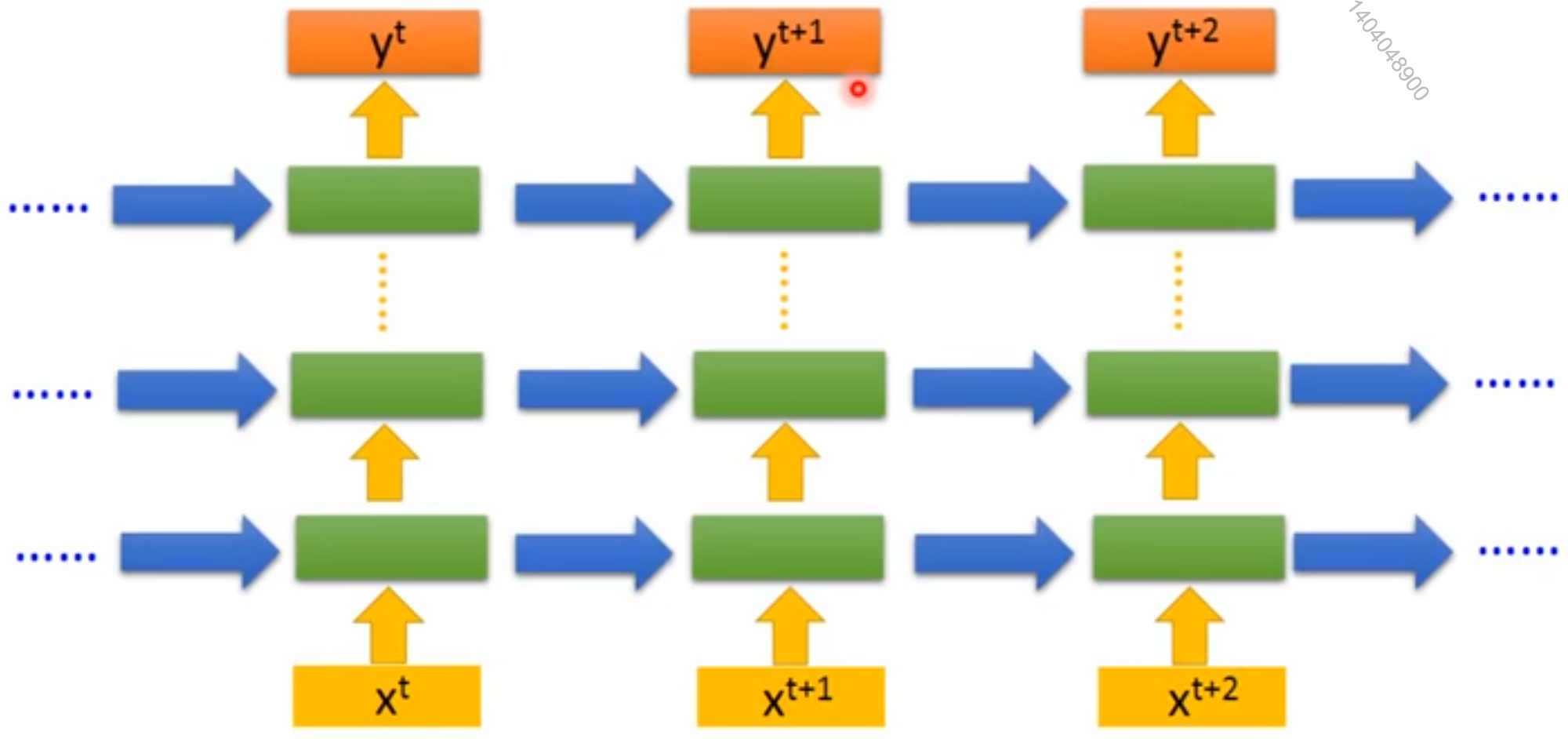
RNN的导数一般比较少，三层都不常见了。
但另一种深度的RNN比较常见：

虽然有多层，但它们之间没有横向连接。
图中每一个框都是一个GRU或LSTM等Unit。

在一般情况下，更容易优化较浅的架构，加入图10.13(b)的额外深度导致从时间步$t$的变量到时间步$t+1$的最短路径变得更长。

[warning] 为什么会路径变长呢？展开不是这样吗？

例如，如果具有单个隐藏层的MLP被用于状态到状态的转换，那么与图10.3相比，我们就会加倍任何两个不同时间步变量之间最短路径的长度。

[warning] “隐藏层用于状态到状态的转换”是什么意思？

然而{Pascanu-et-al-ICLR2014}认为，在隐藏到隐藏的路径中引入跳跃连接可以缓和这个问题，如图10.13(c)所示。

[warning] 怎么看出跳跃连接的？