1. Linear Unit解决二分类问题的局限性

许多任务需要预测二值型变量$y$的值。 具有两个类的分类问题可以归结为这种形式。

此时最大似然的方法是定义$y$在$x$条件下的Bernoulli分布。

[success] 问：什么是“$y$在$x$条件下的Bernoulli分布”？
答：
$\begin{aligned} P(y|x) \sim \phi(y|x;p) \\ P(y=1|x) = p \\ P(y=0|x) = 1-p \end{aligned}$

Bernoulli分布仅需单个参数来定义。 神经网络只需要预测$P(y =1\mid x)$即可。 为了使这个数是有效的概率，它必须处在区间$[0, 1]$中。

为满足该约束条件需要一些细致的设计工作。 假设我们打算使用线性单元，并且通过阈值来限制它成为一个有效的概率：

$P(y=1 \mid x) = \max \left \{ 0, \min \{1, w^\top h+b \} \right \}$

这的确定义了一个有效的条件概率分布，但我们无法使用梯度下降来高效地训练它。 当$w^\top h+b$处于单位区间外时，模型的输出对其参数的梯度都将为${0}$。 梯度为${0}$通常是有问题的，因为学习算法对于如何改善相应的参数不再具有指导意义。

[success] 梯度为${0}$对如何改善算法参数没有指导意义。
Linear Unit不适用于解决二分类问题，这可能是Linear Unit + Cross Entropy做手写数据识别效果不好的原因。

相反，最好是使用一种新的方法来保证无论何时模型给出了错误的答案时，总能有一个较大的梯度。 这种方法是基于使用sigmoid输出单元结合最大似然来实现的。

2. 什么是Sigmoid Unit

sigmoid输出单元定义为

$\hat{y} = \sigma \left (w^\top h + b \right )$

这里$\sigma$是第3.10节中介绍的logistic sigmoid函数。

[success] logistic sigmoid

我们可以认为sigmoid输出单元具有两个部分。 首先，它使用一个线性层来计算$z=w^\top h+b$。 接着，它使用sigmoid激活函数将$z$转化成概率。

我们暂时忽略对于$x$的依赖性，只讨论如何用$z$的值来定义$y$的概率分布。 sigmoid可以通过构造一个非归一化（和不为1）的概率分布$\tilde{P}(y)$来得到。

[success] 问：什么是“非归一化（和不为1）的概率分布”？
答：$0 \le \tilde{P}(y) \le 1$，但不保证$\tilde{P}(y=0) + \tilde{P}(y=1) = 1$。

我们可以随后除以一个合适的常数来得到有效的概率分布。 如果我们假定非归一化的对数概率对$y$和$z$是线性的，可以对它取指数来得到非归一化的概率。

[success] 问：什么是对数概率？
答：将概率取对数，这里是指$\log \tilde{P}$。

[warning] 为什么要假设$\log \tilde{P} = yz$，是否可以有别的假设？

我们然后对它归一化，可以发现这服从Bernoulli分布，该分布受$z$的sigmoid变换控制：

$\begin{aligned} \log \tilde{P}(y) &= yz,\\ \tilde{P}(y) &= \exp(yz),\\ P(y) &= \frac{\exp(yz)}{\sum_{y' = 0}^1 \exp(y' z)},\\ P(y) &= \sigma((2y-1)z). \end{aligned}$

[success]
$\tilde{P}(y)$是非归一化的概率分布。
$P(y)$是归一化后的Bernoulli分布。

基于指数和归一化的概率分布在统计建模的文献中很常见。 用于定义这种二值型变量分布的变量$z$被称为分对数。

3. Sigmoid Unit的交叉熵损失函数

这种在对数空间里预测概率的方法可以很自然地使用最大似然学习。 因为用于最大似然的代价函数是$-\log P(y\mid x)$，代价函数中的log抵消了sigmoid中的exp。

[success] 问：交叉熵代价函数怎么抵消sigmoid中的exp?
答：根据上面的公式得： $\begin{aligned} p_\text{model}(y=1)= \sigma(z) \\ p_\text{model}(y=0)= \sigma(-z) \end{aligned}$

将上面两个式子整合到一起：
$p_\text{model}(y\mid x) = \sigma(z)^y * (1-\log\sigma(z)^{1-y}$

将$p_\text{model}(y\mid z)$代入代价函数得：
$J(x) = - y\log\sigma(z) - (1-y)(1-\log\sigma(z))$

根据求导链式法则：
$\frac{\partial J}{\partial z} = \sigma(z) - y$

导数中消除了$\sigma'$这一部分，从而避免了饱和问题。
link证明了这一点

如果没有这个效果，sigmoid的饱和性会阻止基于梯度的学习做出好的改进。 我们使用最大似然来学习一个由sigmoid参数化的Bernoulli分布，它的损失函数为

$\begin{aligned} J(\theta) &= -\log P(y\mid x)\\ &= -\log \sigma ((2y-1)z)\\ &= \zeta((1-2y)z). \end{aligned}$

这个推导使用了第3.10节中的一些性质。
[success] $\zeta$函数、softplut函数、相关性质

通过将损失函数写成softplus函数的形式，我们可以看到它仅仅在$(1-2y)z$取绝对值非常大的负值时才会饱和。

[success] $\zeta$函数的形状如图所示：

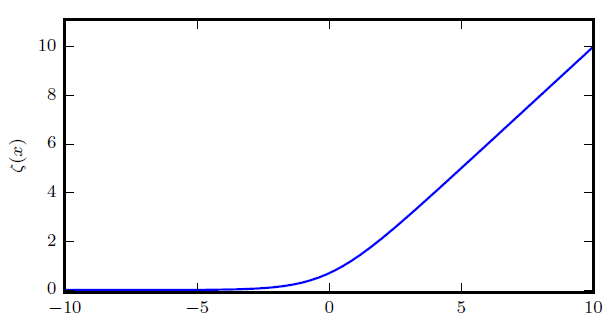
看图可知，只有(1-2y)z && |(1-2y)z|非常大时才会饱和。

因此饱和只会出现在模型已经得到正确答案时——当$y=1$且$z$取非常大的正值时，或者$y=0$且$z$取非常小的负值时。

[success]

1. y=1 $z > 0$ |z|非常大
2. y=0 $z < 0$ |z|非常大
   但只有在已经得到正确答案时会满足这些条件。

当$z$的符号错误时，softplus函数的变量$(1-2y)z$可以简化为$|z|$。 当$|z|$变得很大并且$z$的符号错误时，softplus函数渐近地趋向于它的变量$|z|$。 对$z$求导则渐近地趋向于$\text{sign}(z)$，所以，对于极限情况下极度不正确的$z$，softplus函数完全不会收缩梯度。

[success] 当z符号错误（对应为预测错误）时，不管错误多严重，导数始终为1或-1。
与之对比的是，如果使用二次代价函数，当错误很严重时unit会饱和。

这个性质很有用，因为它意味着基于梯度的学习可以很快地改正错误的$z$。

当我们使用其他的损失函数，例如均方误差之类的，损失函数会在$\sigma(z)$饱和时饱和。 sigmoid激活函数在$z$取非常小的负值时会饱和到0，当$z$取非常大的正值时会饱和到1。 这种情况一旦发生，梯度会变得非常小以至于不能用来学习，无论此时模型给出的是正确还是错误的答案。 因此，最大似然几乎总是训练sigmoid输出单元的优选方法。

4. 下溢问题

理论上，sigmoid的对数总是确定和有限的，因为sigmoid的返回值总是被限制在**开区间$(0, 1)**$上，而不是使用整个闭区间$[0, 1]$的有效概率。

[warning] “sigmoid的对数总是确定和有限的”是什么意思？

在软件实现时，为了避免数值问题，最好将负的对数似然写作$z$的函数，而不是$\hat{y}=\sigma(z)$的函数。

[warning] [?] 这一段看不懂

如果sigmoid函数下溢到零，那么之后对$\hat{y}$取对数会得到负无穷。

[warning] $\hat{y}$不就是$\sigma(z)$吗？怎么会得到负无穷呢？