微积分中的链式法则（为了不与概率中的链式法则相混淆）用于计算复合函数的导数。 反向传播是一种计算链式法则的算法，使用高效的特定运算顺序。

1. 变量是实数

设$x$是实数，$f$和$g$是从实数映射到实数的函数。 假设$y=g(x)$并且$z=f(g(x))=f(y)$。 那么链式法则是说
$\begin{aligned} \frac{dz}{dx}=\frac{dz}{dy} \frac{dy}{dx} && (6.44) \end{aligned}$

[success]
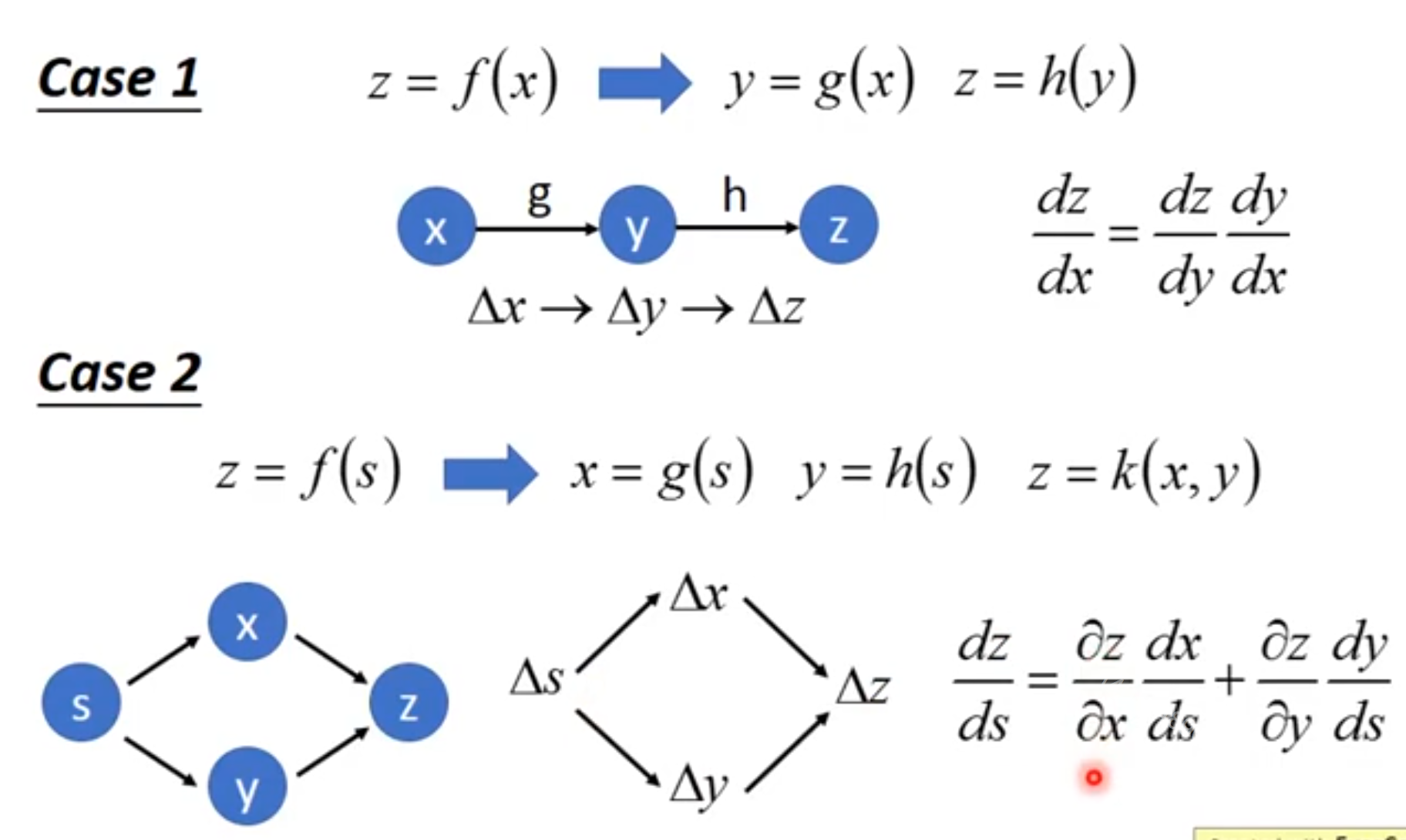同一条链路上两个相邻结点之间的偏导相乘
多条并行链路上的偏导结果相加
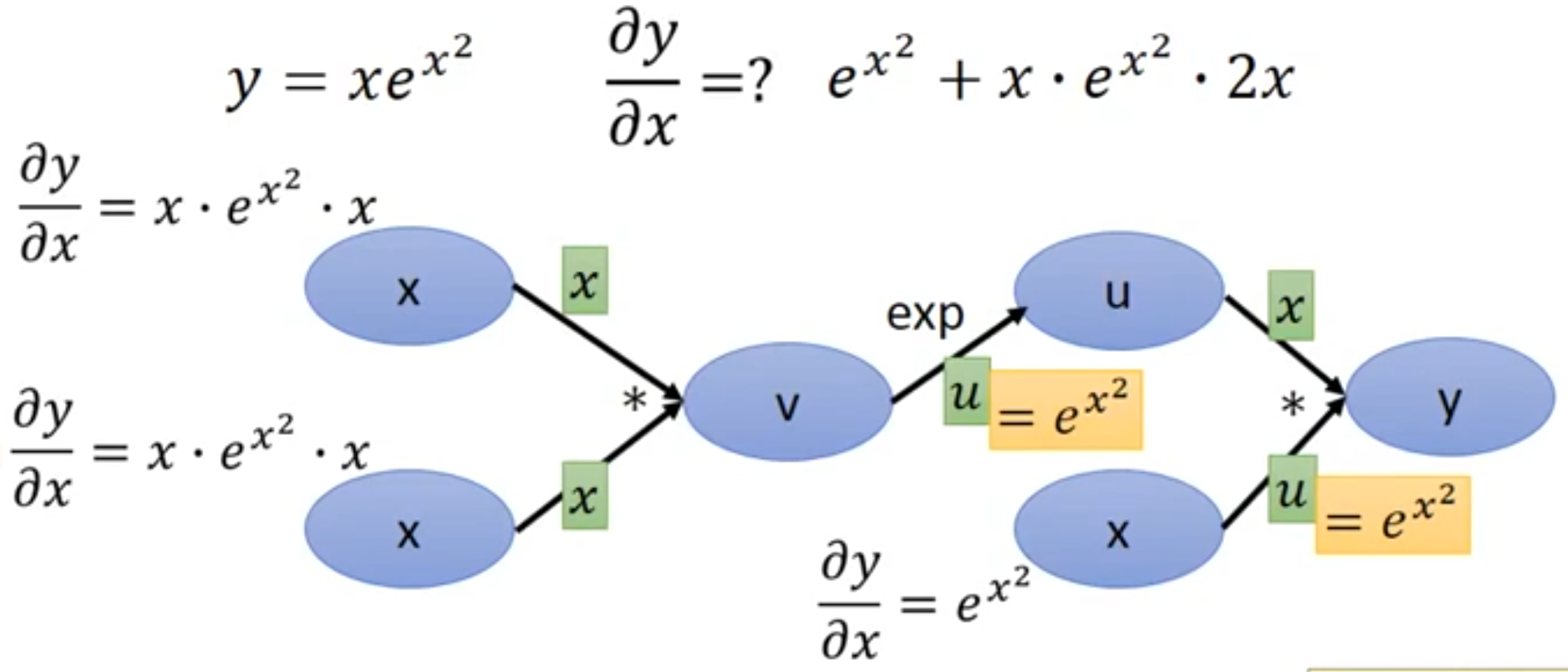
参数共享的情况，先把3个x当作不同的x来看，算完以后再结果全部加起来。

2. 变量是向量

我们可以将这种标量情况进行扩展。 假设$x\in R^m, y\in R^n$，$g$是从$R^m$到$R^n$的映射，$f$是从$R^n$到$R$的映射。 如果$y=g(x)$并且$z=f(y)$，那么
$\begin{aligned} \frac{\partial z}{\partial x_i} = \sum_j \frac{\partial z}{\partial y_j} \frac{\partial y_j}{\partial x_i} \end{aligned}$

[success]
相当于从$x_i$出发，通过多条路径(所有的$y_j$)到达z。
多条并行的链路是相加的关系。

使用向量记法，可以等价地写成
$\begin{aligned} \nabla_{x}z = \left ( \frac{\partial y}{\partial x} \right )^\top \nabla_{y} z && (6.46) \end{aligned}$

这里$\frac{\partial y}{\partial x}$是$g$的$n\times m$的Jacobian矩阵。

[success]
公式6.46可以看作是公式6.44的高维形式。
$\frac{dz}{dy}$中的z是标量，y是向量，向量对标量的偏导仍是向量，记做$\nabla_{y} z$
$\frac{dy}{dx}$中的y是n维向量，x是m维向量，向量对向量的偏导是Jacobian矩阵，矩阵大小为$n\times m$。

从这里我们看到，变量$x$的梯度可以通过Jacobian矩阵$\frac{\partial y}{\partial x}$和梯度$\nabla_{y} z$相乘来得到。 反向传播算法由图中每一个这样的Jacobian梯度的乘积操作所组成。

3. 变量是张量

[warning] 为什么跳过了变量是矩阵

通常我们将反向传播算法应用于任意维度的张量，而不仅仅用于向量。

[success]
这里的“反向传播算法”是指逆着计算图箭头的方向批量计算偏导的过程。（见6.5.3）
不限于前馈网络中的backprop算法。

从概念上讲，这与使用向量的反向传播完全相同。 唯一的区别是如何将数字排列成网格以形成张量。 我们可以想象，在我们运行反向传播之前，将每个张量变平为一个向量，计算一个向量值梯度，然后将该梯度重新构造成一个张量。 从这种重新排列的观点上看，反向传播仍然只是将Jacobian乘以梯度。

[warning] ?[?] 这一段看不懂

为了表示值$z$关于张量$X$的梯度，我们记为$\nabla_X z$，就像$X$是向量一样。 $X$的索引现在有多个坐标——例如，一个3维的张量由三个坐标索引。 我们可以通过使用单个变量$i$来表示完整的索引元组，从而完全抽象出来。 对所有可能的元组$i$，$(\nabla_X z)_i$给出$\frac{\partial z}{\partial X_i}$。 这与向量中索引的方式完全一致，$(\nabla_{x} z)_i$给出$\frac{\partial z}{\partial x_i}$。 使用这种记法，我们可以写出适用于张量的链式法则。 如果$Y=g(X)$并且$z=f(Y)$，那么
$\begin{aligned} \nabla_X z = \sum_j (\nabla_X Y_j)\frac{\partial z}{\partial Y_j} \end{aligned}$

[warning] ?[?] 这一段看不懂