李宏毅补充： 监督学习的数据是labelled data。
半监督学习的数据是：一组labelled data + 一组unlabelled data，且后者数量远大于前者

• transductive learning： unlabelled data是测试数据
• inductive learning： unlabelled data不是测试数据
  为什么有半监督学习？：
• unlabelled data比labelled data便宜。
• 半监督学习符合人类学习过程

半监督学习通道包含人对数据的假设，基于不同的假设会衍生不同的学习方法。学习结果的好坏与“假设是否符合事实”相关。

1. 半监督生成模型

1.1. 监督学习生成模型

先回顾一个监督学习中的生成模型
假设有这样一组二分类的labelled data。

1. 计算先验估计$P(C_i)$
2. 假设条件函数$P(x|C_i) \sim \Bbb N(\mu_i, \Sigma)$，$\Bbb N$代表高斯分布
3. 计算$\mu_i, \Sigma$，例如本例中得出这样的分布：
   
4. 评估新数据属于Ci的概率：
   $P(C_i|x) = \frac{P(x|C_i)P(C_i)}{\sum_iP(x|C_i)P(C_i)}$

1.2. 半监督学习生成模型

将由监督学习生成的模型参数定义为$\theta$
此时又来了一组unlabelled data，用$x^u$表示。原来的labelled data则用$x^r$表示。
基于unlabelled data校正模型。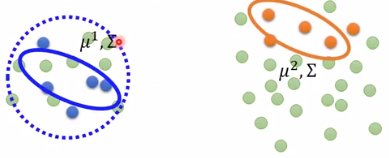

1. 根据参数$\theta$，评估每个unlabelled data属于每个类别的概率$P_\theta(C_i|x^u)$
2. 更新模型参数
   $\begin{aligned} P(C_i) &=& \frac{N_i + \sum_{x^u}P(C_i|x^u)}{N} && (1) \\ \mu_i &=& \frac{1}{N_i}x^r + \frac{1}{\sum_{x^u}P(C_i|x^u)}\sum_{x^u}P(C_i|x^u)x^u && (2) \end{aligned}$

公式说明：
（1）：第一项为labelled data的真实概率。第二项为unlabelled data的期望概率。
（2）：[?]这个公式很奇怪

1. goto 1，直至收敛。

这是一种EM算法，E是第1步，代表Expectation。M是第2步，代表Maximization。
算法过程跟KMeans有点像，区别是初始$\theta$不是随机值，而是labelled data生成的值。

2. 假设一：Low-density Separation 非黑即白

假设数据是可以分开的，即交界处没有数据（low-density）。

2.1. 算法一：self-training

1. 基于labelled data得到模型f*。
2. 用f*对unlabelled data做标记。
3. 把一部分置信度比较高的unlabelled data转成labelled data。
   缺点：只能用于分类问题，不能用于回归问题。因为第2步算出来的label不会导致f*的更新。

self-training VS generative model:
hard label：在self-training算法中，unlabelled data的label一但确定了，就不会再修改。
soft label：在generative model算法中，unlabelled data的label一直在调整。

上面的第1步“基于labelled data得到模型f*”可以使用NN来做。，此时必须用hard label。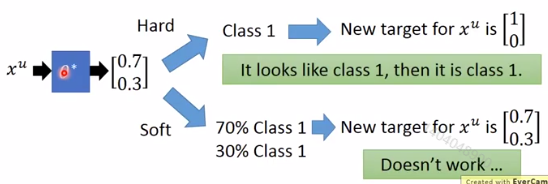

2.2. 算法二：Entropy-based Regularization

原理：输入$x^u$为单个unlabelled data，经过参数为$\theta^*$的模型，得到输出$y^u$为这个data属于哪个分类的概率分布。关键于在怎么判断$y^u$的好坏，并依此来制定代价函数。
Entropy-based Regularization认为：
好：$y^u$分布集中于某一个类别（低熵）。
坏：$y^u$分布平均分布在各种类别上（高熵）。
依此制定的低价函数为：
$\begin{aligned} L = \sum_{x^r}C(y^r, \hat y^r) + \lambda\sum_{x^u}E(y^u) \\ E(y^u) = -\sum_m y_m^u \ln(y_m^u) \end{aligned}$

公式说明：
L的第一项表示：对每个labelled data，期望它的预测值和真实值的差距越小越好。$x^r$为labelled data。C为监督学习分类问题的代价函数，常用的CrossEntropy。
L的第二项表示：对每个unlabelled data，期望它的预测结果越确定越好。结果的确定性用熵公式E来表示。
E用于计算一个分布的熵，m为类别。$y_m^u$为$x^u$属于类别m的概率。

2.3. 算法三：半监督SVM

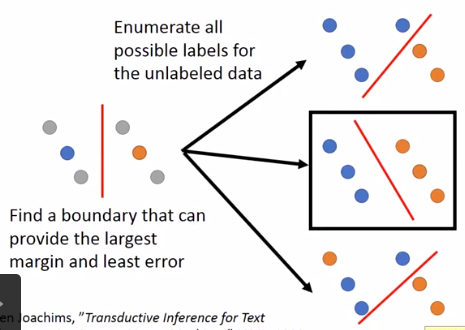
原理：
找到一个提供最大margin和最小error的边界

1. 穷举unlabell data所有可能的label组合。
2. 对每个结果做一个SVM
3. 找到margin最大且error最小的版本
   

3. 假设二：Smoothness Assumption 近朱者赤，近墨者黑

假设：

1. x的分布是不平均的
2. x1、x2在high density region很接近，或者说，x1和x2 connected by a high density path，则y1=y2。
   例如：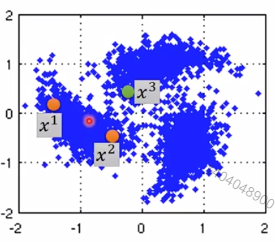
   
   x2和x3更接近，但它们之间没有high density path。
   x1和x2之间有high density path，因此认为y1=y2。
   真实例子：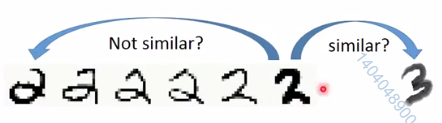
   

3.1. 算法一：Clustering

1. 对数据做cluster
2. 每个cluster的data分作一类（数据量大才有用）
   

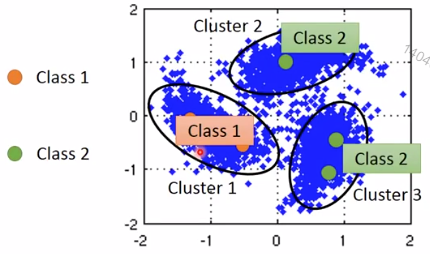
3.2. 算法二：Graph-based Approach

1. 找数据关系
   例如利用网页间的超链接来描述网页间的关系
   利用论文间的引用关系来描述论文
   或者自己定义xi、xj之间的相似度。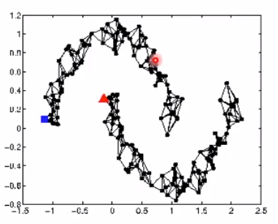
   
2. 建边
   例如KNN、e-Neighbour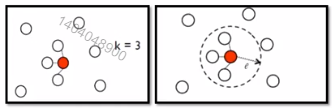
   

3. 定义边的权重
   例如高斯径向基函数：
   $d(x_i, x_j) = \exp(-\gamma||x_i-x_j||^2)$

4. 给unlabelled data分类
   分类依据：labelled data通过Edge的weight影响附近unlabelled data的分类。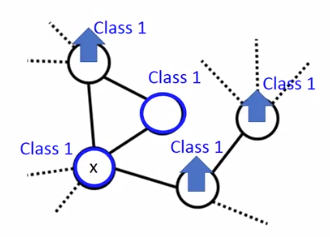
   

5. 通过对分类结果的评价（代价函数）调整NN有参数
   根据算法的假设前提，认为分类结果越smooth说明算法越好。
   定义smoothness:
   $\begin{aligned} S &=& \frac{1}{2}\sum_{i,j}W_{i,j}(y_i-j_j)^2 && (1) \\ &=& y^\top L y && (2) \\ y &=& [y^r | y^u]^\top && (3) \\ L &=& D - W && (4) \\ Lost &=& \sum_{x^r}C(y^r, \hat y^r) + \lambda S && (5) \end{aligned}$

公式解释：
（1）：计算Smoothness，值越小越好。$W_{i,j}$代表遍历所有的数据对，包含labelled data和unlabelled data。如果x1、x2之间的权重大，则希望y1、y2尽量地接近。如果x1、x2之间的权重小，则y1、y2之间的关系不重要。
（2）：公式（1）的进一步推导。（3）、（4）是对（2）的补充。
（4）：L不是lost function，而是Graph Laplacian矩阵。D是一个对角矩阵，且$D_{i,i} = \sum_j W_{i,j}$
（5）：代价函数。第一项用于labelled data，与上文中的[Entropy-based Regularization]相同。第二项用于判断整体数据的smoothness。

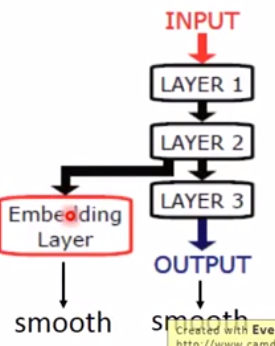
Note:
在NN模型中，S的计算不一定要放在lost function上，也可以放在NN的任意一层。

3.3. 算法三：Better Representation 去芜存菁 化繁为简