1. 2.3 性能度量

目的：衡量模型泛化能力和评价标准

回归任务的度量：

均方误差 - mean squared error - MSE

$E(f;D) = \frac{1}{m}\sum_{i=1}^m(f(x_i) - y_i)^2$

f：模型 D：数据
$f(x_i)$ ：预测结果
$y_i$ ：真实标记

$E(f;D) = \int_{x \sim D}(f(x)-y)^2p(x)dx$

D：数据分布
p(x)：概率密度函数

分类任务的度量

错误率、精度、查准率、查全率

1.1. 2.3.1 错误率和精度

$\begin{aligned} E(f;D) &=& \frac{1}{m} \sum_{i=1}^mI(f(x_i) \neq y_i) \\ acc(f;D) &=& \frac{1}{m} \sum_{i=1}^mI(f(x_i) = y_i) &=& 1 - E(f;D) \\ E(f;D) &=& \int_{x \sim D}I(f(x)\neq y)p(x)dx \\ acc(f;D) &=& \int_{x \sim D}I(f(x) = y)p(x)dx &=& 1-E(f;D) \end{aligned}$

1.2. 2.3.2 查准率、查全率与F1

查准率 = precision = 准确率：挑出的正例中有多少真的是正例
查全率 = recall = 召回率：多少正例被挑出来了

1.2.1. 混淆矩阵

横：预测纵：真实	P	N
P	TP	FN
N	FP	TN

T：真实=预测
F：真实！=预测
P：正例
N：负例

查准率 $P = \frac{TP}{TP+FP}$
查全率 $R = \frac{TP}{TP+FN}$

对同一个模型来说，P和R是矛盾的度量

1.2.2. P-R曲线

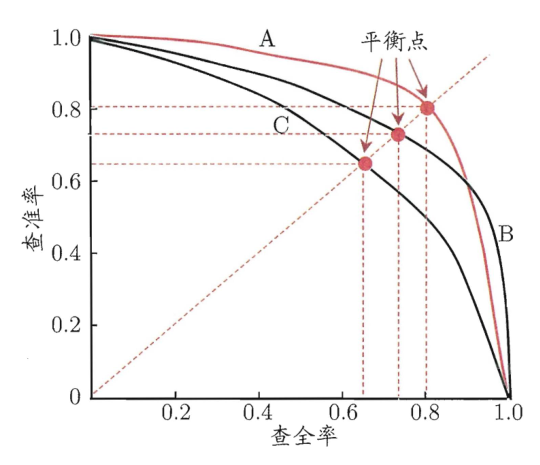
根据P-R曲线比较两个模型的好坏：

若曲线不交叉（例如B和C），则外侧曲线的对应的模型B优于内侧曲线对应的模型
若曲线交叉（例如A和B），则只能在具体的条件下比较
比较曲线下面的面积，大则优
比较平衡点（Break-Even Point）的值，P=R时的值，大则优
F1度量，调和平均
$F1 = \frac{2 \times P \times R}{P + R} = \frac{2 \times TP}{\text{样本数} + TP - TN}$
$F_\beta$ 度量，加权调和平均
$F_\beta = \frac{(1+\beta^2)\times P \times R}{(\beta^2 \times P) + R}$

$\beta < 1$ ：更注重查准率
$\beta = 1$ ：相当于F1
$\beta > 1$ ：更注重查全率

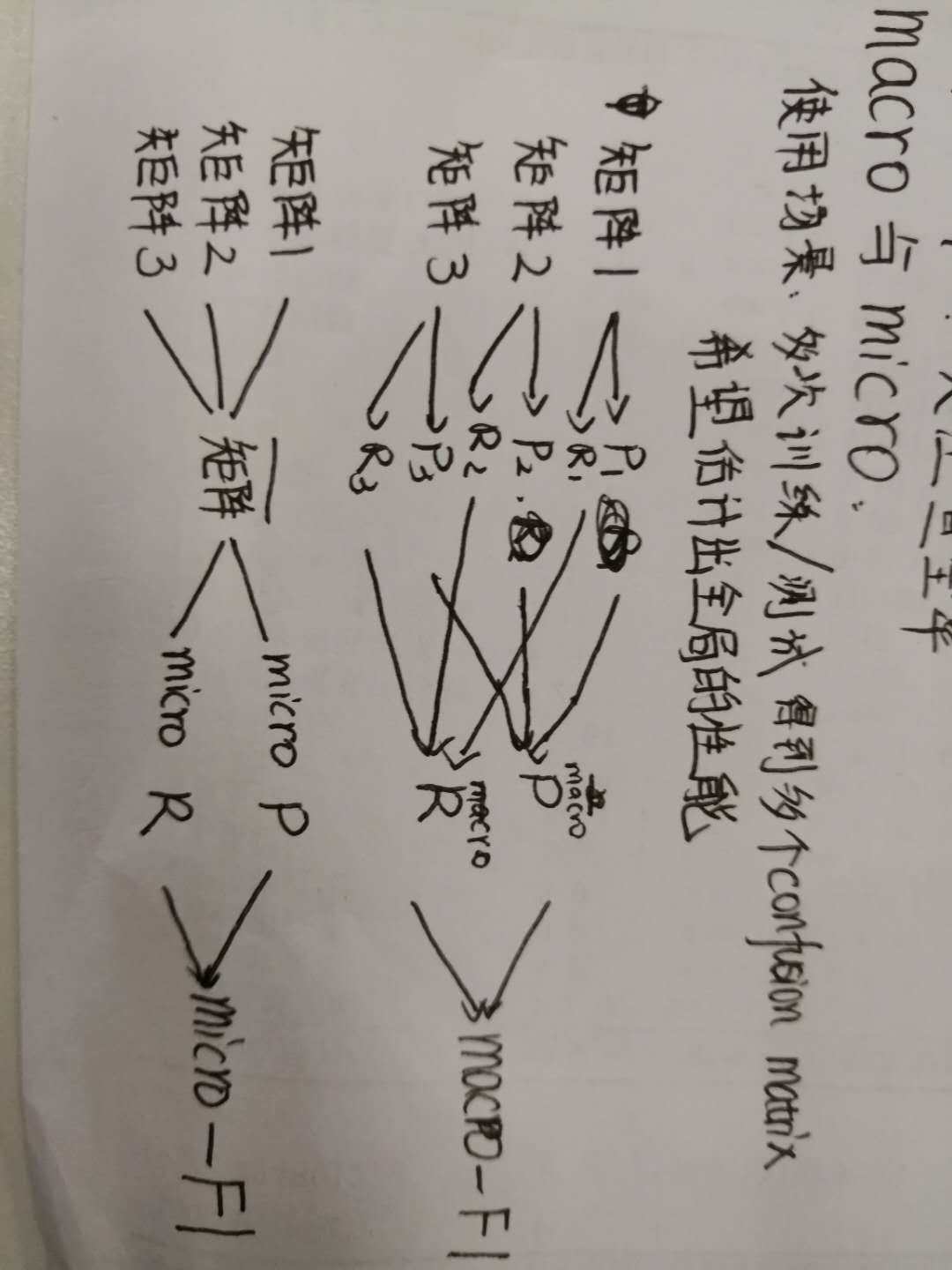
1.2.3. macro与micro

使用场景：多次训练/测试得到多个confusion matrix，希望能估计出全局的性能

1.3. 2.3.3 ROC与AUC

把预测结果根据是正类的概率排序，排序本身的质量好坏，体现了“一般情况下”泛化能力的好坏。

真正例率：正例中预测正确的比例
$TPR = \frac{TP}{TP+FN}$

假正例率：负例中预测错误的比例
$FPR = \frac{FP}{TN+FP}$

ROC曲线：由TPR和FPR组成的曲线
AUC：Aera Under Curve，ROC曲线下面的面积

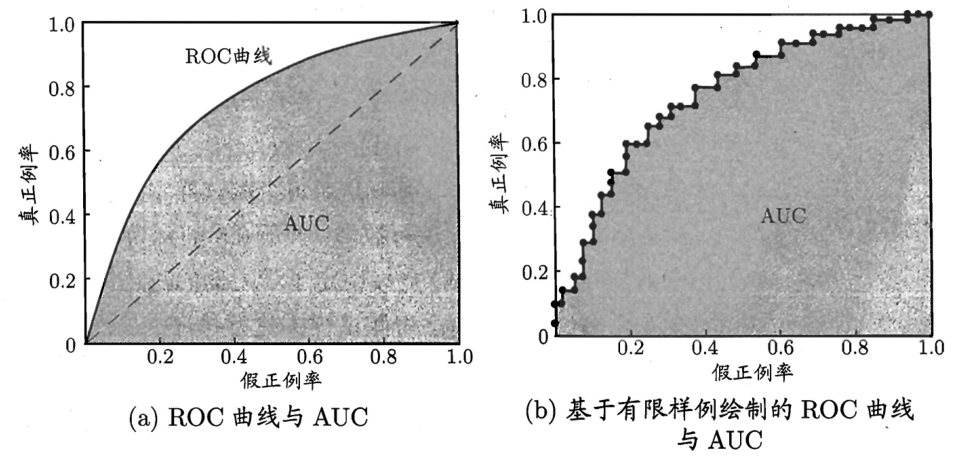
$AUC = \frac{1}{2}\sum_{i=1}^{m-1}(X_{i+1}-X_i)\cdot (y_i+y_{i+1})$

[?]为什么是 $frac{1}{2}(y_i+y_{i+1})$ ？这种情况下应该 $y_i=y_{i+1}$

1.4. 2.3.4 代价敏感错误率与代价曲线

代价矩阵 cost matrix
最小化错误次数 --- 最小化“总体代价”
ROC曲线 --- 代价曲线 cost curve

2.3 性能度量